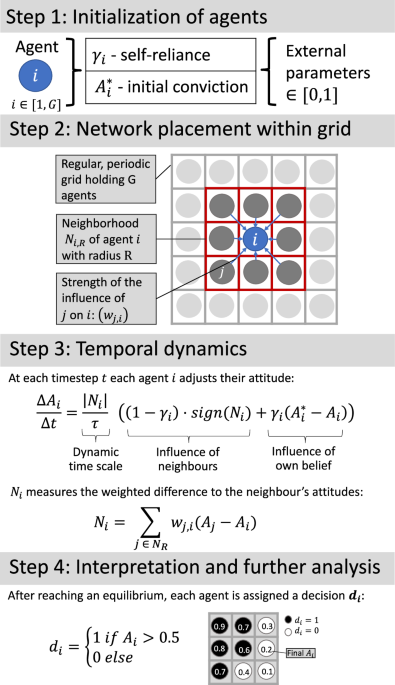
In this ABM, we explore the polarization of opinion due to the opposing forces of individualism and group affiliation. We formalize individuality by assigning each agent a continuous “independence” parameter, γ, that represents the extent to which the agent depends on others in forming its opinion (Figure 1). This runs on a continuum from 0 (“very dependent”) to 1 (“very independent”). In addition, each agent has an initial belief \({A}_{i}^{* }\) that represents its unique opinion on the topic, scaled continuously from 0 (‘completely disagree’) to 1 (‘completely agree’). Both parameters are uniformly distributed in the basic version of the model. The agents are then randomly placed on a regular, periodic grid with G agents (100 × 100 agents by default, G = 10,000). All qualitative results are obtained by averaging the model ensemble of 100 different initial distributions. Each agent is equally influenced by its eight surrounding neighbors, i.e., its Moore neighborhood of radius 1. In step 1, each agent updates its attitude A based on the independence-weighted influence of neighboring agents and the difference between its own opinion and that of its neighbors (see Figure 1). Once the model completes the final time step and reaches a steady state, each agent is assigned a final attitude of either 0 or 1, determined by a specified threshold (default is 0.5) for its final attitude. makes the final decision on. This model setup is simple but has multiple advantages. First, the number of agents, their sizes, the weighting of neighborhood influences, and the parameter distributions are modular and therefore easily adjustable. Second, it depends on very few input parameters: the degree of independence γ and the initial belief \({A}_{i}^{* }\). Opinion generation (the transition from initial belief to final attitude) is not subject to externally specified thresholds, and all observed polarization emerges. Finally, the interpretation is understandable, allowing an unobstructed view of the mechanism of independence.
Figure 1: Model setup and dynamics.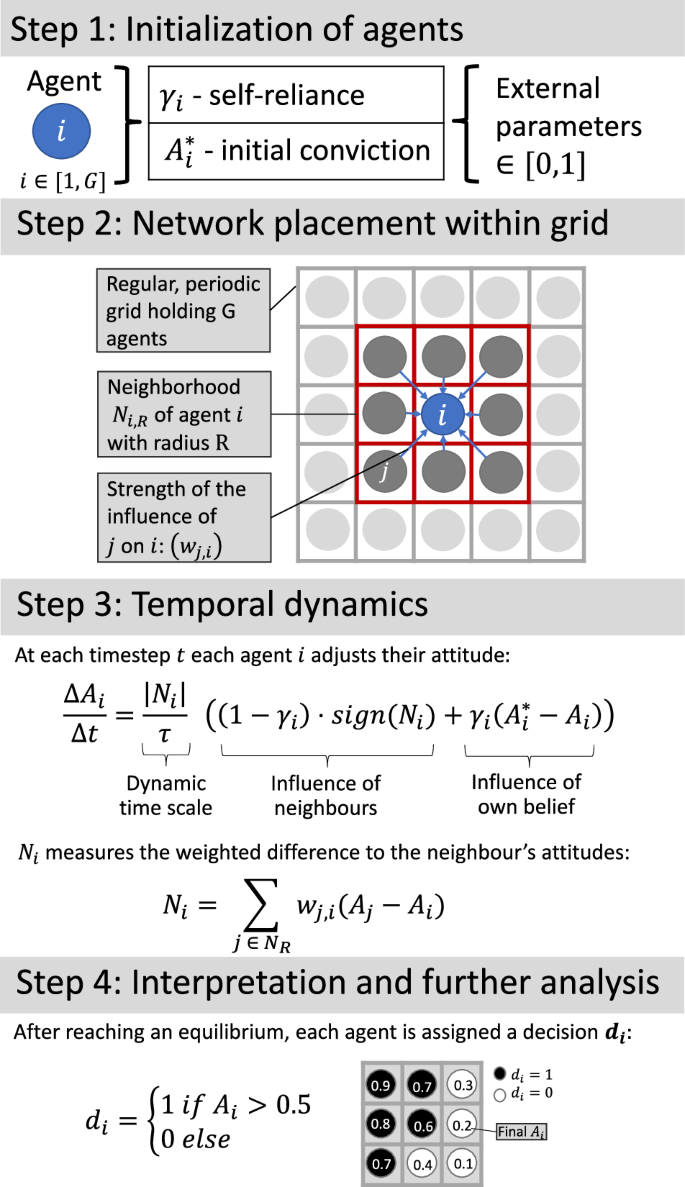
Agents are initialized with degrees of independence γi, which represent individualism, and initial beliefs \({A}_{i}^{* }\), which are also the starting values for attitudes Ai. Agents are placed on a regular periodic grid with G agents (default size 100 × 100, G = 10,000 agents) and assigned neighbors based on Chebyshev distance. The default specification uses a Moore neighborhood with Chebyshev distance 1, i.e. radius 1. At each time step, agents form attitudes Ai with dynamics that take into account the influence of the neighborhood and the efforts of the agents towards their initial beliefs, both of which are influenced by independence. Once an equilibrium is reached, each agent is assigned a final decision. Both the final opinion and the final decision are used for further analysis.
Technical model description
Here we present the technical details of the model described above. The structure and dynamics of the model are shown in Figure 1. We assume that each agent has two time-invariant attributes: the initial belief \({A}_{i}^{* }\in [0,1]\) and the degree of independence γi ∈[0, 1]represents the agent’s desire for individualism, with γi = 1 corresponding to individualistic opinion formation and γi = 0 implying opinion formation purely driven by social neighborhood. Furthermore, each agent’s current opinion is described by a time-varying attitude parameter Ai ∈[0, 1]which evolves as described in equation (1). To initialize agent i at t = 0, its attitude is initialized to its initial belief \({A}_{i}^{* }={A}_{i}(0)\). \({A}_{i}^{* }\) and γi are drawn from independent random distributions. As a variation of our model, we provide additional results for the case where the initial belief \({A}_{i}^{* }\) and the initial attitude Ai(0) are independent of each other (Supplementary Figs. 22–25).
Agent i interacts with a set of neighbors Mi. In a simple example on a grid with periodic boundaries, i.e. a torus, all agents j with Chebyshev distance \({d}_{C}:= \max ({x}_{j}-{x}_{i},{y}_{j}-{y}_{i})\le 1\) with agent i are part of the neighborhood Mi. This is also known as a Moore neighborhood of radius 1. The strength of j's influence on i is given by the weights wj,i, which for simplicity we assume to be constant as \({w}_{j,i}:=\frac{1}{\#{M}_{i}}\,\forall \,i,j\). For application of the modeling framework on network structures, these assumptions can be relaxed in the implementation of the open source model. Regarding robustness, we also show the results for neighborhoods up to dC ≤ 2 in Supplementary Figures 30–32, which show qualitatively robust results with only minor variations.
A simple example of agent evolution is shown in Supplementary Figure 1. At each time step t, agent i adjusts its attitude Ai according to the difference between its neighbors' average attitude (defined by its neighbors' influence Ni) weighted by 1 − γi and its initial belief \({A}_{i}^{* }\) weighted by γi∣Ni∣. To avoid noise due to continuous updates of agents' attitudes, all agents update their attitudes simultaneously at time t based on their own attitudes and the attitudes of their neighbors at the previous time step t − 1. The independence term is proportional to the difference in the attitudes of their neighbors. Thus, the more your opinion differs from that of your neighbors, the more the influence of your initial belief is. Including the time scale τ, the dynamics of Ai is expressed as follows:
$$\begin{array}{ll}\frac{{{\Delta }}{A}_{i}}{{{\Delta }}t}\,=\,\frac{| {N}_{i}
(1)
The neighborhood influence is defined as \({N}_{i}
(2)
The derivation of the equilibrium conditions is given in the “Equilibrium Conditions” section of the Supplementary Material, and results in two qualitatively different equilibria.
$${N}_{i}=0\,{{{\rm{ and }}}}\,{A}_{i}^{* }-{A}_{i}=\frac{1-{\gamma }_{i}}{{\gamma }_{i}}{{{\rm{sign}}}}\left({N}_{i}\right).$$
(3)
Measures of self-actualization and social cohesion
Decision alignment as a measure of self-actualization
Here, we understand self-actualization to be the degree to which an agent follows its personal initial beliefs. To formalize this, we consider the alignment between the initial beliefs and the final decision the agent makes after exposure to the influence of its neighbors. To this end, we define the initial decision \(\tilde{{d}_{i}}\) of agent i as \(\tilde{{d}_{i}}:= {{{{\bf{1}}}}}_{{A}_{i}^{* }\ > \ 0.5}\), where \({A}_{i}^{* }\) is the initial belief. Recall that the final decision di is defined as \({d}_{i}={{{{\bf{1}}}}}_{{A}_{i}\ > \ 0.5}\). The decision alignment can then be stated as follows:
$${\delta }_{i}:= {{{{\bf{1}}}}}}_{{d}_{i} = \tilde{{d}_{i}}}.$$
(Four)
Thus, positive decision alignment is achieved if the initial belief and the final decision lead the agent to the same binary choice. The social self-actualization level is calculated as the average decision alignment and is formally expressed as:
$${{\Delta }}:= \frac{{\sum }_{i}{\delta }_{i}}{G},$$
(5)
where G is the total number of agents. Figure 5 shows how the level of social self-actualization varies with the average level of independence.
In addition to these empirical results, we can also analytically derive how the average decision alignment Δ depends on the distribution of the independence γi using a mean field approximation approach. This means that we derive the average outcome for society using the simplifying assumption of independence of Ai and Ni, which is only true when considering the average across society, not for individual agents. Specifically, based on the possible equilibria identified in equation (3) above, we approximate the expected decision alignment of agent i by its independence γi. The expected value of δi at the final equilibrium state can be estimated as follows:
$$\begin{array}{ll}{{\Delta}}={\mathbb{E}}\left[{\delta }_{i}\right]\,=\,\left[{\mathbb{P}}({N}_{i} < 0)+{\mathbb{P}}({N}_{i} \,>\, 0)\right]\left[\frac{1}{2}+{\mathbb{P}}\left({{{\mathcal{U}}}}(0,0.5) \,>\, \frac{1-{\gamma }_{i}}{{\gamma }_{i}}\right)\right]+\frac{1}{2}{\mathbb{P}}({N}_{i}=0)\\\qquad\qquad\quad \,=\,\frac{1}{2}+\left[{\mathbb{P}}({N}_{i}\,\ne\, 0)\right]{\mathbb{P}}\left({{{\mathcal{U}}}}(0,0.5) > \frac{1-{\gamma }_{i}}{{\gamma }_{i}}\right)\end{array}$$
(6)
Considering that \({\mathbb{P}}\left({{{\mathcal{U}}}}(0,0.5) > \frac{1-{\gamma }_{i}}{{\gamma }_{i}}\right)\), it follows that only individuals in \({\gamma }_{i}\ge \frac{2}{3}\) can contribute to this term.
$$0.5\ge \frac{1-{\gamma }_{i}}{{\gamma }_{i}}\iff 0.5{\gamma }_{i}\ge 1-{\gamma }_{i}\iff {\gamma }_{i}\ge \frac{2}{3}$$
This approximation of the mean-decision alignment allows us to compare the simulation results with the analytical expectation, as shown in Figure 5. A detailed derivation of this expected mean-decision alignment (Eq. (6)) is given in the Supplementary Material (Detailed Derivation of Eq. (6)).
The prevalence of opinions as a measure of social cohesion
To measure social cohesion, we consider the spread of opinions ω between the two extremes of society as the difference between the 90th and 10th percentiles of final attitudes. That is, for \({{\mathbb{A}}}_{final}\), which represents the final attitudes of all agents, we have
$$\omega := Pc{t}_{90}({{\mathbb{A}}}_{final})-Pc{t}_{10}({{\mathbb{A}}}_{final}).$$
(7)
Thus, when opinion divergence is high, the distance between the extreme ends of the opinion spectrum is large, implying a low sense of belonging to the society represented by the average opinion. Moreover, high opinion divergence may be an obstacle in determining common beneficial solutions. Therefore, we interpret high opinion divergence as indicating low social cohesion and low opinion divergence as indicating high social cohesion.
For robustness, we also present results for different percentile thresholds of opinion spread in the Supplementary Information, as referenced in the Results.