The GTAP-DynW model is a large-dimensional CGE model that uses the large-scale GTAP (Global Trade Analysis Project) database version 1057, where countries and regions import and exchange goods and services with each other. GTAP-DynW is an intertemporal CGE model (looking forward) rather than a recursive CGE model, and includes 18 agro-economic zones58 that characterize the climate, soil and topographic conditions relevant to agricultural production.59 Following Kompas and Van Ha16 and Kompas et al.15, the model also includes a climate change damage function.
In GTAP-DynW, in each country or region, producers combine inputs (land, labor, capital, intermediate goods, and natural resources) to produce a single good or service, which is then consumed domestically by local households (final consumption) and producers (intermediate demand as an input in the production of other goods) or exported to other international or regional households and producers. Producers consider future impacts and policy settings according to the following system of equations of motion:
$${\dot{k}}_{r,t}={\varphi }_{r,t-}{\delta }_{r}{k}_{r,t}$$
(1)
$${\dot{\mu}}_{r,t}={\mu}_{r,t}\left[{{i}_{t}+\delta }_{r}\right]-\frac{{\phi }_{r}}{2}{\left(\frac{{\psi }_{r}}{{k}_{r,t}}\right)}^{2}{p}_{r,t}^{I}-{p}_{r,t}^{K}$$
(2)
where \({p}_{r,t}^{K}\) and kr,t are the rental price and capital stock of region r at time t. \({p}_{r,t}^{I}\) is the price of investment goods. δr is the capital depreciation rate. ψr is the capital growth due to (gross) investment activity, which is the overall interest rate. \({\phi }_{r}\) is the investment growth coefficient. µr,t is the shadow price of capital.
Effects of water stress
Agricultural production (Qj,t) is approximated by a constant elastic substitution (CES) production function that includes the use of commodity i by j from both domestic and imported sources (QFi,j,t) and the value added of industry j (QVAj,t).The demand for value added of industry j (QVAj,t) by endowments including the 18 AEZ land use categories and natural resources (QSEi,j,t) is expressed as follows:
$${QSE}_{i,j,t}=\left[\frac{{QVA}_{j,t}}{{afe}_{i,j,t}}\right]{\left({afe}_{i,j,t}\frac{{PVA}_{j,t}}{{PSE}_{i,j,t}}\right)}^{{\gamma }_{j,t}}$$
(3)
where afei,j,t is the increase in technical change in endowment i due to j, PSEi,j,t is the market price of “stagnant” endowment i (e.g., land that is difficult to reallocate) used in industry j, PV Aj,t is the value-added price of firms in industry j, and γj,t is the elasticity of transformation of stagnant primary factor endowments in value-added production in j.
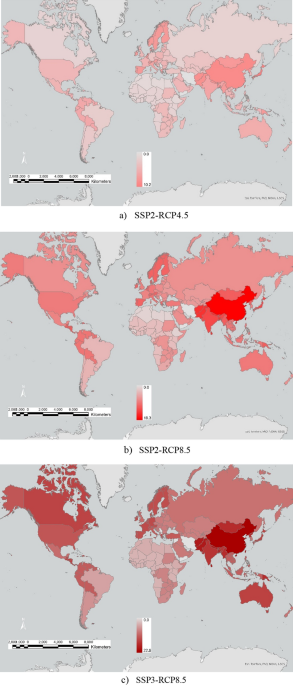
Under the influence of water and heat stress, climate change reduces the effectiveness of agriculture and land use in AEZs, with the relative decrease in efficiency of land endowments being directly proportional to the relative increase in water stress. In GTAP-DynW, water stress is taken from WRI60. This global GIS water data for 15,006 basins was spatially joined with the global GIS layer Esri-USGS61 to generate geographic water stress projections for 174 countries, which were then mapped to the total of 30 countries/regions in GTAP-DynW. Water stress at a point in time due to region i is estimated from the projections of water stress for all basins j in region i, using a weighting factor for j measured as the area or percentage of j in the total basin area of i.
$$ws\left(i\right)={\sum }_{i=1}^{J}wsb\left(i,j\right)\frac{B\left(i,j\right)}{{\sum }_{i=1}^{J}B\left(i,j\right)}$$
(Four)
where wsb(i, j) is the water stress of basin j (in the set of J basins located in region i), where i belongs to one of the 30 regions (I) of GTAP-DynW, and B(i, j) is the area of basin j located in i.
Water stress impacts land use by AEZs by region and time with QFEi,j,t, changing QVAj,t and thus agricultural production (Qj,t). The water stress indicator is the deviation (i.e. too much, too little) from the 2020 baseline under the impact of climate change according to WRI60 and is quantified only for irrigated agriculture. The magnitude of the water stress shock by AEZs depends on the share of irrigated land in the total land use in the AEZs of a region (wc,irr) and the change in irrigation water volume in that AEZ in the region (dIWc,t) and is expressed as:
$$QSE_{i,j,t} = \mathop {\overbrace{{\frac{{L\left( {c,irr} \right)}}{{L\left( {c} \right)}}}}}\limits^{{w{_c,{irr}} }}{{dIW_{c,t} }}$$
(5)
where c, j, and t represent land type, agricultural product, and time for the 18 AEZs.
To calibrate the impact of water stress on agricultural production, we assumed a constant elasticity of substitution (CES) production function and defined the demand for intermediate inputs (QFi,j,t) as:
$${QF}_{i,j,t}=\left[{A}_{i,j,t}\frac{{Q}_{j,t}}{{afw2}_{j,t}{\left(\frac{{pf}_{i,j,t}}{{afw1}_{i,t}}\frac{1}{{ps}_{j,t}}\right)}^{{\gamma }_{j,t}}}\right]$$
(6)
where Qj,t is the agricultural output of commodity j, pfi,j,t is the firm price of input commodity i used by j, psj,t is the supply price of commodity j, Ai,j,t is the composite regional variable driving technological change, and γj,t is the elasticity of substitution between composite intermediate inputs in agricultural sector j. Two specific technological change driving variables are the water stress coefficients for intermediate inputs and endowments used in production (afw1i,t) and the region-specific average rates of intermediate inputs driving technological change in j (afw2j,t).
Shock afw1c,j,t is the weighting factor of irrigated land in total land use of agricultural crops wirr,j, the change in irrigation water use over time (dIWc,t), and the water stress factor for crop yield, or
$$dafw1_{c,j,t} = \mathop {\overbrace{{\frac{{L\left( {c,j,irr} \right)}}{{L\left( {c,j} \right)}}}}}\limits^{{w_{irr,j} }} \frac{1}{{dIW_{c,t} }}ws_{c,j,t}$$
(7)
where c, j, and t represent land types, agricultural products, and time in the 18 AEZs. The price of water paid by industries using water from water resources adds to the region's income but also increases the costs of these sectors, which may cause a shift or reallocation of water use among water-using industries. For a water price pwater
(8)
where VFAj,k,r,t is the purchase and business tax of k input commodities used by sector j, pj,k,r,t is the market price of k relative to j, taxFj,k,r,t is the tax on business purchases of k from production j, pwaterr,t is the price of water at t and WINj,k,r,t is the water intensity of j relative to k. Thus, a water stress shock induces a change in PFEj,k,r,t and a shift in water withdrawals from domestic and imported sources depends on the mix of domestic and imported commodities.
Effects of heat stress
Damage functions show the relationship between climate variables (e.g., mean temperature, humidity, and hot days) and productivity, income, and resource endowments62. Roson and Sartori62 provide parameter estimates for damage functions for six climate impacts: sea level rise, crop yield variability, heat stress impacts on labor productivity, human health, tourism, and household energy demand, for 120 GTAP countries and regions using GTAP9. GTAP-DynW projections include damage functions related to heat stress in the agricultural sector and its impacts on agricultural output and labor productivity, using GTAP10a. Global warming-induced heat stress shocks (e.g., agricultural and labor productivity losses) are based on Kompas et al.15, Kompas and Van Ha16, and Roson and Sartori62.
Impact on food security
In GTAP-DynW, each food has a nutrient content with a different energy intake (calories). The total nutrient supply (measured as gigacalories (GCal)) in a region r (S(r,t)) is determined by the food production i or
$$S\left(r,t\right)={\sum }_{i=1}^{I}\frac{S\left(i,r,t\right)z\left(i\right)*1000}{{10}^{9}}$$
(9)
where S(i, r, t) is the amount of food production i (thousand tons), z(i) is the nutrient conversion factor for food i to calculate the energy content of one ton of food i into calories. The average daily nutrient intake a required for human food security is known and varies between countries and regions (source data: FAO22,63,64).
$$F\left(r,t\right)=\frac{S\left(r,t\right)*{10}^{9}}{a*365*{10}^{6}}$$
(Ten)
where a is the average daily nutrition in calories, world food production (GCal) is the sum of food supplies across all regions, and the total population across regions is F(r,t).
The number of people (in millions) who are severely food insecure is determined by the difference between minimum caloric demand and available production, and can be expressed as:
$$IF\left( {r,t} \right) = \mathop {\frac{{\overbrace{{\left[ {S(r,0) – S(r,t)} \right]}}10^{9} }}{{a*365*10^{6} }}}\limits^{{ds\left( {r,t} \right)}}$$
(11)
where dS(r, t) is the reduction in food production in region r to the base nutrient supply (S(r, 0)) at time t.
The food insecurity ratio (RIF(r, t)) is the ratio of the number of people with severe food insecurity to the total population of a country or POP (r, t).
$$RIF\left(r,t\right)=\frac{IF\left(r,t\right)}{POP\left(r,t\right)}$$
(12)
The decline in world food production (dS
Source link